IainM
Landlord.
So, chilling the last few degrees to get to pitching temperature can be painfully slow, especially if you are brewing in the summer, doing a lager, don't have the time to no-chill, or don't have a counter-flow chiller or brew fridge. Perhaps you just want to get the yeast in there as soon as possible. One way of getting there is to make the wort a little more concentrated, chill part way, and then use ice to bring the brew down to pitching temp. To avoid the risk of infecting your uninoculated wort with cubes from the freezer drawer you can freeze an unopened bottle of water, of known volume (2L, 1L, 750ml, 500ml...), and cut the plastic off and chuck it in when needed. Knowing the volume of water can help you plan your OG. The question is, at what temperature should you add the ice cube in order to exactly hit your pitching temperature? This is actually a very straight forward calculation.
So,
T_pitch is the pitching temperature you want, in Celsius.
T_ice is the temperature of your freezer, in Celsius.
V_ice is the volume of water in the bottle you froze, in litres.
V_bulk is the volume of wort to which you are going to add the ice, in litres.
T_add is the temperature you need to cool down to before putting the ice in, in Celsius.
The equation, then is:
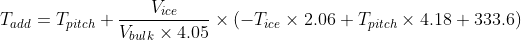
To give an example, image you want to get 18 litres of lager wort at a pitching temperature of 10C, by adding a frozen 2L bottle of water from freezer (at -5C) to 16L of wort of more concentrated wort. In this case Tpitch = 10, Tice = -3, Vbulk = 16 and Vice = 2. Putting these in gives you Tadd = 10 + 0.031 * (6.18 + 41.8 + 333.6) = 21.8. So, you can chill your wort down to 21.8C, put in the 2L of frozen water, give it a stir to melt it, and you end up with 18 litres of wort at 10C, ready to pitch and ferment. I've tried this out a couple of times, and it works very well. In practice, this is all you need to know, but in the next post I'll put a bit of theory for those that might be curious as to why the equation works, and why it is the way it is.
So,
T_pitch is the pitching temperature you want, in Celsius.
T_ice is the temperature of your freezer, in Celsius.
V_ice is the volume of water in the bottle you froze, in litres.
V_bulk is the volume of wort to which you are going to add the ice, in litres.
T_add is the temperature you need to cool down to before putting the ice in, in Celsius.
The equation, then is:
To give an example, image you want to get 18 litres of lager wort at a pitching temperature of 10C, by adding a frozen 2L bottle of water from freezer (at -5C) to 16L of wort of more concentrated wort. In this case Tpitch = 10, Tice = -3, Vbulk = 16 and Vice = 2. Putting these in gives you Tadd = 10 + 0.031 * (6.18 + 41.8 + 333.6) = 21.8. So, you can chill your wort down to 21.8C, put in the 2L of frozen water, give it a stir to melt it, and you end up with 18 litres of wort at 10C, ready to pitch and ferment. I've tried this out a couple of times, and it works very well. In practice, this is all you need to know, but in the next post I'll put a bit of theory for those that might be curious as to why the equation works, and why it is the way it is.



